| |
田中 (2017), p.13
|
気圧とは単位面積あたり (メートル単位でいえば1m2) の空気の鉛直コラムの重さのことである。
|
|
ひとには,この説明がすんなり入るらしい。
これは,水圧モデルの説明である。
気象学は気圧モデルを一応押さえているふうであるが,いざ気圧を説明し出すと,上に引用したようになる。
空気圧は, 「空気分子の壁との衝突」で説明される。
よって大気圧も, 「空気分子の壁との衝突」で説明することになる。
即ち,「地表の単位面積に空気分子が衝突するその大きさ」として。
そこで本当なら,つぎの疑問が持たれるはずなのである:
この2つは同じものなのか?
a. 地表の単位面積に空気分子が衝突するその大きさ
b. 地表の単位面積に鉛直な空気コラムの重さ
a と b の関係は自明ではない。
自明でないと思う者は,自分で確かめねばならなくなる。
空気分子の質量を \( m \),分子量を \( a \) とする。
単位面積の地表の面 \( S \) と,\( S \) に鉛直な高さ \( x \) の空気コラム \( C_x \) を考える。
\( C_x \) の空気分子密度を \( \rho( x ) \) とする。
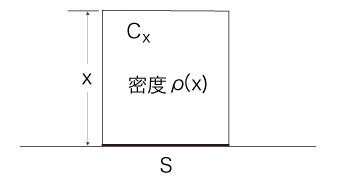
\( C_x \) に理想気体の状態方程式を適用する。
\( C_x \) の体積は,\( C_x \) の底面 \( S \) の面積が単位面積なので,\( x \) 単位体積。
よって \( C_x \) の重さが,\( \rho(x) \ x \) 単位重さ。
よって \( C_x \) のモル数が,
\[
\frac{ \rho(x)\ x }{a}
\]
以上より,つぎが \( C_x \) に対する理想気体の状態方程式になる:
\[
p(x) \ x = \frac{ \rho(x)\ x }{a}\ \ R\ T(x)
\]
\( R \) :モル気体定数
即ち,
\[
p(x) = \frac{R}{a}\ \rho(x)\ T(x)
\]
\( \rho(x) \) は,グラフがつぎのような形の関数になる:
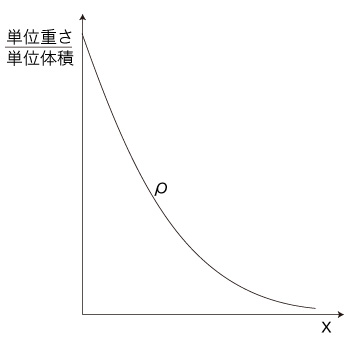
「空気の分子量は 28.8」「1モルの気体の体積は, 常温常圧で約 22.4リットル = 0.0224 m3」より,
\[ \rho( 0 ) = ( 28.8 / 1000 ) / 0.0224 \approx 1.3 kg /m^3
\]
そして \( T(x) \) は,つぎの類の図が示す気温 (絶対温度) である:
田中 (2017), p.11 から引用
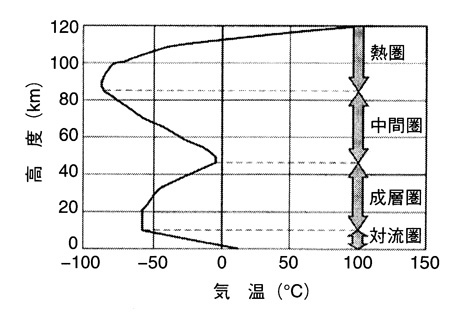
さて,比べたいのはつぎの2つであった:
a. 地表の単位面積に空気分子が衝突するその大きさ
b. 地表の単位面積に鉛直な空気コラムの重さ
a の計算式は:
\( x \) の変化に対する \( p(x) \) の変化率を \( p'(x) \) とするとき,
\[
\int_0^{x} p'(x)\,dx = p(x) - p(0) = \frac{R}{a}\ \rho(x)\ T(x) - p(0) \\
\ \\
p'(x) = \frac{d}{dx} \bigl( \frac{R}{a}\ \rho(x)\ T(x) \bigr) = \frac{R}{a}\ \frac{d}{dx} \bigl( \rho(x)\ T(x) \bigr)
\]
よって,
\[
p(0) = \frac{R}{a}\ \rho(x)\ T(x) - \frac{R}{a} \int_0^{x} \frac{d}{dx} \bigl( \rho(x)\ T(x) \bigr) \ dx
\]
b の計算式は:
\[
\int_0^{x} \rho (x)\,dx
\]
計算では,xに適当に十分な大きさの値を入れる。
a は,十分な大きさのxに対して
\[
\frac{R}{a}\ \rho(x)\ T(x) \approx 0
\]
なので,
\[
p(0) = - \frac{R}{a} \int_0^{x} \frac{d}{dx} \bigl( \rho(x)\ T(x) \bigr) \ dx
\]
2つの計算式
\[
- \frac{R}{a} \int_0^{x} \frac{d}{dx} \bigl( \rho(x)\ T(x) \bigr) \ dx \\
\int_0^{x} \rho (x)\,dx
\]
は,同じ値を出すというものではない。
ということは?
「気圧とは単位面積あたりの空気の鉛直コラムの重さのこと」は嘘だということである。
「地上気圧は頭上の空気の重さ」と言う者は,気圧を水圧モデルで考えているのである。
気圧モデルは,水圧モデルとは違う。
水圧モデルは,静水圧平衡モデルである。
実際,「地上気圧は空気柱の重さ」にしたいときは,「地上気圧に対し静水圧平衡を仮定する」という言い方になるのである。
- 引用文献
- 田中 博 (2017) :『地球大気の科学』, 共立出版, 2017.
|



 対比:水圧は静水圧平衡モデル
対比:水圧は静水圧平衡モデル