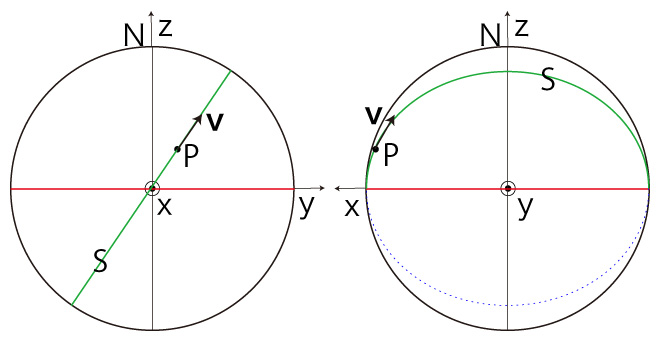
このとき,移動 \( ( P,\ \bf{v} ) \) にはつぎの加速度がかかる:
\[
\begin{align}
( & - \frac{v^2}{R}\ cos( P_a ) - v\ \Omega\ cos( S_a )\ cos( P_a ), \\
& - \frac{v^2}{R}\ cos( S_a )\ sin( P_a ) - v\ \Omega\ sin( P_a ), \\
& - \frac{v^2}{R}\ sin( S_a )\ sin( P_a ) ) \\
\ \\
- ( & - v\ \Omega\ cos( S_a )\ cos( P_a ) - R \Omega^2 \ cos( P_a ), \\
& - v\ \Omega\ sin( P_a ) - R \Omega^2 \ cos(S_a)\ sin( P_a ), \\
& 0 ) \\
\ \\
=\ & \bigl( \
( - \frac{v^2}{R} + R \Omega^2 )\ cos( P_a ), \\
& ( - \frac{v^2}{R} + R \Omega^2 )\ cos(S_a)\ sin( P_a ), \\
& - \frac{v^2}{R}\ sin( S_a )\ sin( P_a ) \
\bigr) \\
\end{align}
\]
加速度は,引き算の式になっている。
なぜ引き算か?
点 \( P \) からの速度 \( \bf{v} \) の移動は,時間 \( \Delta t \) でつぎのようになる:
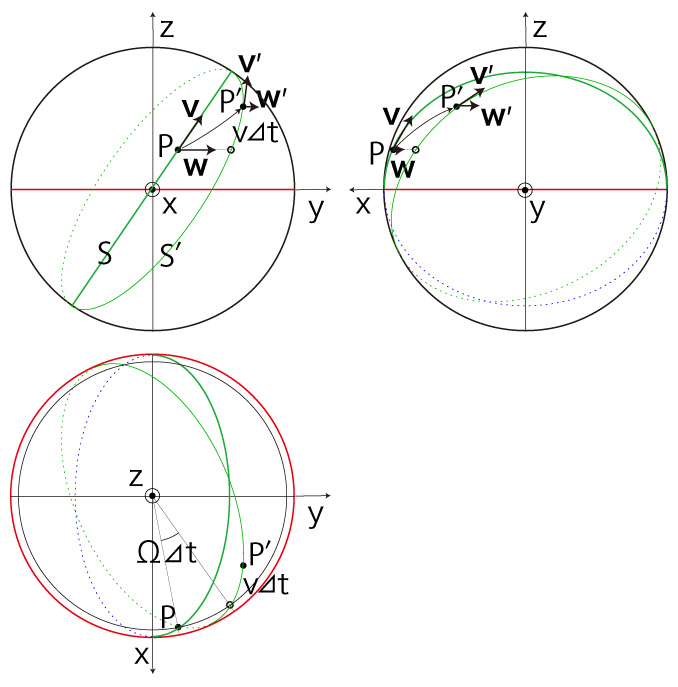
\( {\bf w},\ {\bf w'} \) は,自転球体の回転による移動速度。
ここでひとが間違いやすいのは (実際,気象学は間違うのだが),加速度を求めるために比較しようとする2つの速度
\( P \) における移動速度
\( P' \) における移動速度
の定め方である。
\( P \) における速度と \( P' \) における速度の比較は,自転球体に固定の観察者による比較である。
観測者にとって,点 \( P,\ P' \) は回転していない。
よって,この観測者が比較する速度は, \( {\bf{v}} - {\bf{w}} \) と \( {\bf{v'}} - {\bf{w'}} \) である。
そこで,\( P \) において移動にかかる加速度は,つぎの式になる:
\[
\lim_{t \to 0} \frac{ ( {\bf v'} - {\bf w'} ) - ( {\bf v} - {\bf w} ) }{ \Delta t } \\
= \lim_{t \to 0} \frac{ {\bf v'} - {\bf v} }{ \Delta t }
- \lim_{t \to 0} \frac{ {\bf w'} - {\bf w} }{ \Delta t } \
= \ \frac{ d {\bf v} }{ dt } - \frac{ d {\bf w} }{ dt }
\]
加速度の式の後ろの項
\[
\begin{align}
- \frac{ d {\bf w} }{ dt } =
- ( & - v\ \Omega\ cos( S_a )\ cos( P_a ) - R \Omega^2 \ cos( P_a ), \\
& - v\ \Omega\ sin( P_a ) - R \Omega^2 \ cos(S_a)\ sin( P_a ), \\
& 0 ) \\
\end{align}
\]
は,「遠心力加速度」に見立てられる (「ー」をとると「向心力加速度」)。
これに対し前の項
\[
\begin{align}
\ \ \frac{ d {\bf v} }{ dt } = \
( & - \frac{v^2}{R}\ cos( P_a ) - v\ \Omega\ cos( S_a )\ cos( P_a ), \\
& - \frac{v^2}{R}\ cos( S_a )\ sin( P_a ) - v\ \Omega\ sin( P_a ), \\
& - \frac{v^2}{R}\ sin( S_a )\ sin( P_a ) ) \\
\end{align}
\]
は,\( v = | {\bf v} | \) が一定なので, 「転向力加速度」である。
所謂「コリオリ力 (加速度)」は,これを指していることになる。
翻って,「コリオリ力加速度」で留意すべきは,これは単独では存在しないということである。
これは,遠心力加速度を伴う。
そして,遠心力と合わさってきっちり相殺される部分を含んでいる。
──上式のつぎの部分:
\[
- v\ \Omega\ cos( S_a )\ cos( P_a ) \\
- v\ \Omega\ sin( P_a )
\]
こういうわけで,「コリオリ力」のことばは,ひじょうにミスリーディングである。
実際,気象学は「コリオリ力」を間違う。
気象学は,「空気塊は進行方向と直角の力 (「コリオリ力」) を受けて曲げられる」を教義にしている。
単独では存在しないものを単独で存在するものにしているのである。
「コリオリ力──空気塊は進行方向と直角にはたらいて進路を曲げる力」というものは無い。
これは気象学がつくるフィクションである。
|
 自転円板の場合
自転円板の場合
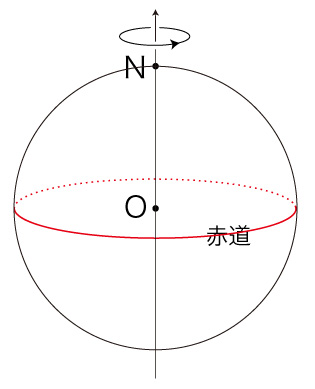
 加速度の \( ( S_a, P_a ) \)-表現 ):
加速度の \( ( S_a, P_a ) \)-表現 ):
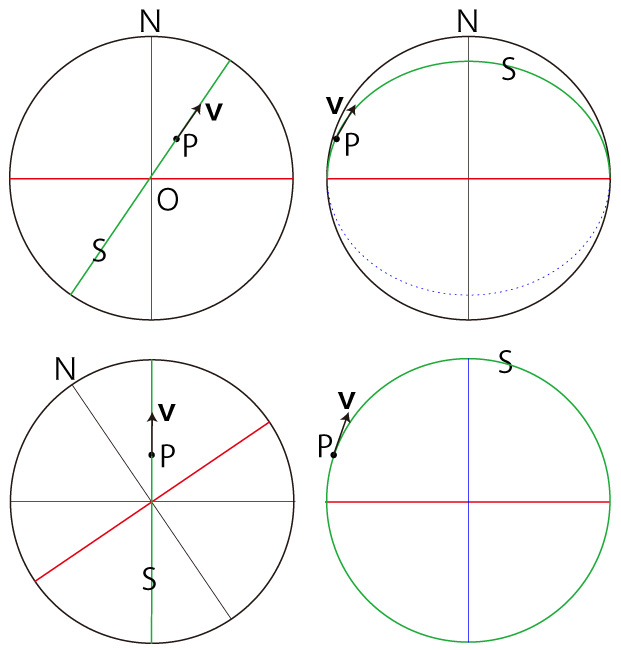
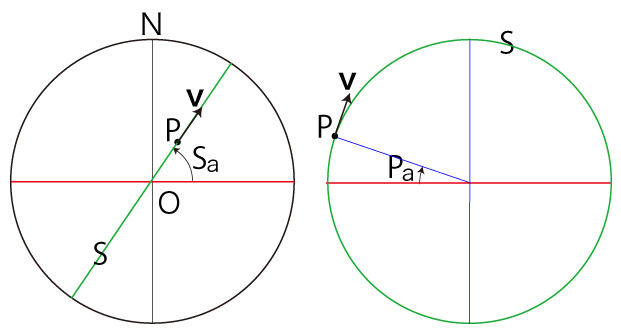
 \( ( P, {\bf{v}} ) \)-座標 ):
\( ( P, {\bf{v}} ) \)-座標 ):