気象学は,偏西風の高速を「角運動量保存」を持ち出して説明する(註)。
これは「角運動量保存」の誤用である。
そして気象学の言いたいことは,応分のロジックで述べることができるものである。
そのロジックを以下に示す。
誤解の無いよう念のため:
論理的に問題の無い形に述べ直しているだけで,偏西風の高速の説明としては間違っている。
──ただのアブストラクト・ナンセンスである。
地球の自転は,地上の点に回転速度を与える。
「風速」とは「地点Pの風速」のことであって,この速度はPの回転速度に対する相対速度である。
地上の点の回転速度を計算してみよう。
地球の半径を \( R \) (m),角速度を \( \Omega \) (ラジアン/秒) とすると,緯度 \( \theta \) (ラジアン) の地点の回転速度 \( v \) (m/秒) は,
\[
\quad \quad v = ( R\ cos( \theta) )\ \Omega
\]
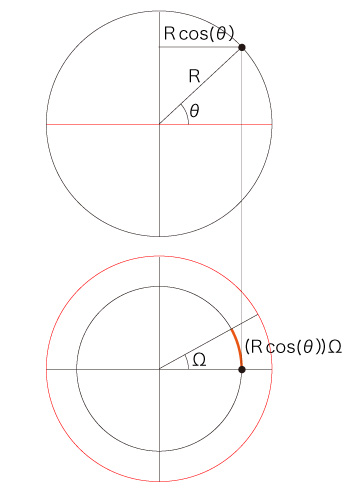
\( R, \Omega \) は,「地球1周 4万km」「1日24時間」を使って,つぎのように計算される:
\[
\quad \quad R = \frac{ 40000 \times 1000 }{ 2 \pi } \\
\ \\
\quad \quad \Omega = \frac{ 2\ \pi }{ 24 \times 60 \times 60 }
\]
よって,
\[
\quad \quad v = ( R\ cos( \theta) )\ \Omega = \frac{ 40000 \times 1000 }{ 24 \times 60 \times 60 } \ \ \ cos( \theta)
\]
これを計算すると,「地上の点の回転速度」がつぎのように得られる:
| 緯度 (°) |
回転速度 (m/秒) |
| 0 |
463 |
| 10 |
456 |
| 20 |
435 |
| 30 |
401 |
| 40 |
355 |
| 50 |
298 |
| 60 |
231 |
| 70 |
158 |
| 80 |
80 |
いま,北緯30度で「無風」を表している空気塊が,南側からの圧によって北緯40度に押し上げられたとしよう。
すると,この空気塊は \( 401 - 355 = 46 \) m/秒 の風になる。
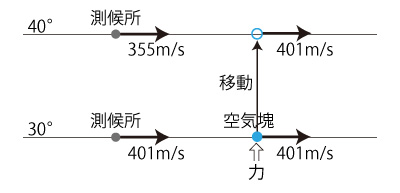
(移動は, 自転する地球に固定した視座で見たもの)
46 m/秒は,けっこうな強風である。
偏西風の高速は,これである。
偏西風の高速は,《低緯度から高緯度に押し上げられた風は,強風になる》で説明されるものである。
|
これが偏西風の高速の説明になっていないのは,低緯度から高緯度に押し上げられる」が,成立しないからである。
気象学は「低緯度から高緯度への風の平行移動」を信じているが,自転球体上の移動がそんなふうになることは無いのである。
註. 例えばつぎのように「角運動量保存」を誤用する:
| |
田中 (2007), pp.50,51
回転する地球表面に束縛された大気には、角運動量の保存則が成り立つ。
これを気象要素で表現すると以下のように書ける。
図2.7のように、たとえば赤道上に地理的に静止していた空気のチューブが、北緯30度まで移動したとする。
ここで、赤道上で静止している空気は、宇宙空聞から見ると地球の自転とともに猛スピードで西から東に移動しており、1日で1周している。
地球の半径を6370キロメートルとするとその空気塊の速度は463メートル毎秒となる。
これは音速よりも速い。
もちろん、空気全体が回っているので、赤道に立っている人にも、音は普通に聞こえるわけである。
したがってこの空気は、速度 × 回転半径 = 463メートル毎秒 × 6370キロメートル の角運動量をもっている。
この空気のチューブが北緯30度まで移動したとすると、回転半径は 6370キロメートルから5517キロメートルに短縮されるので、角運動量保存則からこの空気塊の速度は535メートル毎秒に増大する。
北緯30度の地面の回転速度は401メートル毎秒なので、空気のチューブは地面に対して134メートル毎秒の西風となる。
北緯45度なら328キロメートル毎秒、60度なら696メートル毎秒である。
図2.7 (p.43)
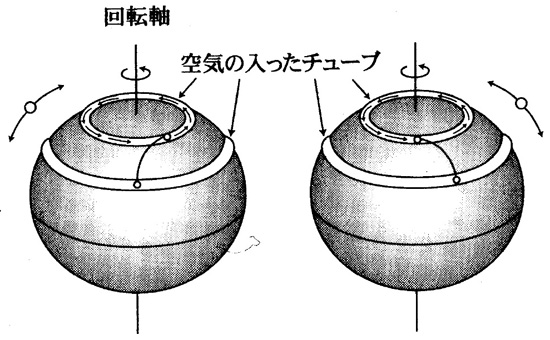
|
|
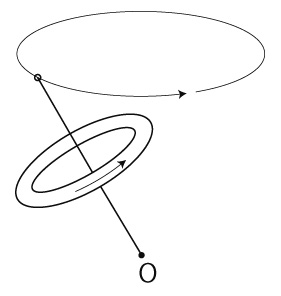
「角運動量」は,コマの話である。
「チューブの角運動量保存」の絵を描けと言われたら,コマになったチューブの絵を描くことになる。
それは, つぎのような絵である:
引用文献
- 田中博 :『偏西風の気象学』(気象尾ブックス016)), 成山堂, 2007.
|

 気象学の嘘 :「コリオリ力・角運動量」
気象学の嘘 :「コリオリ力・角運動量」

